Climbing [B]

Memory limit: 64 MB

The Byteburg University holds a climbing course. 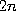students can attend the course simultaneously. Each of the climbers has their own separate climbing route along which they can go either upwards or downwards. The climbers are divided into pairs, with the climbers in each pair climbing on adjacent routes and attached to the same belay rope. Each rope is attached at the top of the wall in a point lying between two routes and should be tense at all times.

The length of each rope is not greater than the height of the climbing wall. When one climber in a pair has reached the top of the wall, the other climber from the pair cannot go downwards.

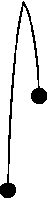
Figure: A pair of climbers attached to a single rope.

Every climber has exactly one adjacent climber to the left and to the right apart from the leftmost and the rightmost climbers who have just one adjacent climber. The climbing instructor has given an exercise to his students: they are to adjust their heights in such a way that there are as many pairs of adjacent climbers from different ropes hanging at the same heights as possible. Help the climbers and find the maximum number of such adjacent climbers.

Input

The first line of the standard input contains one integer (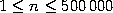) that denotes the number of pairs of climbers. The following lines contain descriptions of climbers from the respective pairs, given from left to right. Each line contains two integers 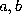(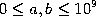) that denote the distances of the climbers in the pair from the point where their rope is attached.

Output

The first and only line of the standard output should contain one integer equal to the maximum number of adjacent pairs of climbers from different ropes that can align at the same height.

Example

For the input data:

3
1 1
3 2
1 4

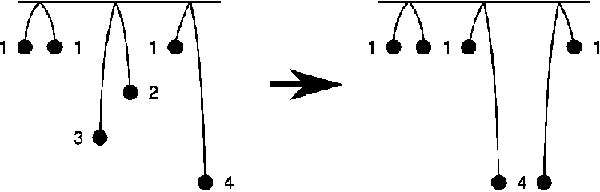
the correct result is:

2

Task author: Jacek Tomasiewicz.